일단 씻고 나가자
24174번 : 알고리즘 수업 - 힙 정렬 2 본문

뉴진스의 하Heap보이요.
수많은 시간초과에 진짜 이를 바득바득 갈며 멘탈이 수없이 나갔던 문제. 구현만 완료하면 문제 자체 내용은 어렵지 않았으나, 시간초과에 컴파일 에러에.. 그만큼 입력과 출력에서 시간을 줄이는 방법에 대해 크나큰 깨달음을 얻은 문제다. 다시는 시간초과로 고통 받고 싶지 않아 정말..


(수도 코드(pseudo code)가 한국말로 의사 코드란 걸 처음 알게 됐다.)
서두에서 말했던 것처럼 의사 코드만 잘 구현하고 추가적인 요구사항만 조금 넣어주면 쉽게 풀 수 있으므로,
의사 코드 자체를 해석하는 시간을 가져보자.
그러려면 Heap이란 무엇인가를 알아야 한다!! 대충만 알아보자!!

힙이란 완전 이진 트리를 베이스로 한 자료구조이며, 완전 이진 트리란 모든 층이 꽉 차 있어야 하진 않지만 그림에서의 1~5 순서대로 왼쪽부터 자식 노드가 차례차례 채워져야 하는 트리이다.
항상 자식 보다 부모가 숫자가 작은 것을 만족하는 힙을 최소 힙이라고 하며(반대는 최대힙), 실제 구현 시엔 인덱스는 1부터 시작, 그리고 부모 노드의 인덱스는 '자식 노드의 인덱스' / 2 의 정수부를 갖는 특징을 가지고 있다. 주의할 점은 같은 레벨에 있는 자식들의 순서는 크기를 보장해주지 않는다는 점이다. 즉, 그림에서 2와 3의 위치가 바뀌어도 트리는 조건을 만족한다.
(+ 문제의 요구사항은 기본적으로 최소 힙의 구현이지만, 보편적인 방법인 트리의 가장 높은 노드를 빼고 다시 트리를 재구성하는 방법 대신 정렬된 배열의 가장 마지막 인덱스와 첫 인덱스 값을 바꿔놓고 다시 트리의 재구성을 요구한다.)

이제 의사 코드를 해석해보자. 대빵이 heap_sort (빨간색) 이고, 이 함수는 어디에서든 호출되지 않으니 최종 실행부라고 생각하면 되겠다. 대빵은 build_min_heap (파란색) 과 heapify (초록색) 두 함수를 모두 호출하고 있으나, heapify (초록색)은 build_min_heap (파란색) 내부에서도 호출되고 있으니 사실상 초록색이 제일 꼬봉이라고 보면 된다.
즉 초록색 -> 파란색 -> 빨간색 순서로 서열이 올라가니, 본 순서대로 해석해보자.
1. heapify(A[], k, n)

매개 변수는 A는 배열, k는 우선 모르겠고, n은 주석에서 최대 인덱스임을 알려주었다.
우선 left, right를 k의 2배와 2배+1 하라는 걸 보니 이진 트리 노드의 인덱스를 설명하는 것이라 쉽게 유추할 수 있다. 즉, k는 부모 노드의 인덱스, left right는 k의 자식 노드의 각각 왼쪽 오른쪽 인덱스이다.
갑자기 right를 n과 비교를 한다?? n은 최대 인덱스랬는데.. 이건 무슨 소린고 하니, 앞서 설명했듯 힙의 이진 트리 구조는 완전 이진 트리로, 트리가 예쁘게 꽉 차 있을 필요는 없다. == 자식 노드가 무조건 두 개가 있을 필요는 없다는 뜻이다.
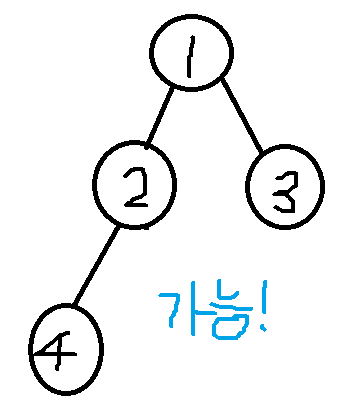
즉 그림처럼 트리의 가장 마지막 노드가 누군가(2)의 왼쪽 노드(4) 하나 뿐이어도 완전 이진 트리의 조건은 성립하기 때문에, 해당 if문으로 트리의 마지막 노드가 왼쪽 노드인지 오른쪽 노드인지 판별하는 작업이 필요하다. (해당 분기를 수행하지 않는다면 있지도 않은 오른쪽 노드의 인덱스에 접근하여 에러를 낼 수 있다.)
위의 그림을 예로 들어 이해해보자. 부모 노드가 2일 때 right는 부모 인덱스의 *2 +1 값이므로 위 그림을 예시로 적용해본다면 2 *2 +1 = 5의 인덱스를 갖게 되지만,
5는 트리의 최대 인덱스 n인 보다도 큰 수로 당연히 존재할 수 없는 인덱스이기 때문에 right 노드는 없음을 알 수 있다.
이렇게 부모 인덱스를 통하여 특정 위치의 자식 인덱스를 계산했을 때 최대 인덱스보다 작은지 큰지 비교를 통하여 자식의 여부를 확인할 수 있다는 내용이 해당 if문의 논리인 것이다.
if(right <= n) 은 마지막 노드(n)가 오른쪽(right)노드라는 뜻이며, 그 뜻은 왼쪽 오른쪽 노드 모두 존재한다는 뜻이고,
if (A[left] < A[right]) // 는 두 자식 중에 어떤 노드의 값이 더 작은지 인덱스를 구하겠다는 뜻이다.
smaller <- left // 만약 해당 조건이 맞다면 더 작은 인덱스(smaller)는 left이고,
smaller <- right // 틀리다면 더 작은 인덱스(smaller)는 right가 되겠다.
else if(left <=n) // 은 마지막 노드(n)가 왼쪽(left)노드라는 뜻이고,
smaller <- left // 왼쪽노드밖에 존재하지 않으므로 당연히 더 작은 인덱스는 left 하나 뿐이다.
else return // 앞의 조건이 모두 성립하지 않는다면 자식 노드가 없다는 소리로 그냥 함수를 빠져나간다.
그렇게 해서 k의 자식 노드 중에 값이 더 작은 자식 노드의 인덱스인 smaller을 구했는데, 자식들 중 더 작은 노드인 A[smaller]가 부모 노드인 A[k]보다 작으면 최소힙의 조건에 맞지 않겠지??? 따라서 자식 노드가 부모 노드보다 작을 시에'만' 실행되는, 부모 노드(k)와 작은 자식 노드(smaller)를 서로 교환해주는 코드가 주석 아래로 위치한 재귀적 코드이다. heapify(A, k, n) 대신 heapify(A, smaller, n)을 수행하여 smaller과 k가 바뀐 이후에도 똑같은 방법으로 smaller의 자식들이 더 작은 값이 없는지 체크한다.

2. build_min_heap(A[], n)

역시 매개 변수에 A 배열, 최대 인덱스인 n을 받고 있다.
for i // 이야 당연히 for(int i = 이겠고..
i <- └ n/2 ┘ // 는 i 가 n/2부터 (n/2를 포함)
downto 1 // 1까지 i-- 하며 해당 루프문을 수행하라는 뜻이다!!
i 값을 앞선 heapify의 k 위치에 넣었는데, k는 앞서 부모 노드의 인덱스라는 의미였었다. 즉 함수 이름처럼 배열을 최소 힙 구조가 되도록 내부 값들을 재조정 하는 과정으로, 부모 노드에 n/2 부터 1까지 넣어보며 검사하는 기능을 구현하고 있다. n/2가 최초 검사 인덱스인 이유는 n은 최대 인덱스이고, n이 마지막 노드라면 당연히 n의 자식 노드는 없을 것이며, 마지막 노드의 부모 노드 인덱스는 n/2 일 것이므로, 가장 마지막 '부모 노드'인 인덱스부터 가장 최상위 노드인 1까지 검사하며 바꿔가는 과정인 것이다~~
3. heap_sort(A[])

마지막으로 최종 수행 코드인 대빵이!
대빵이는 배열 하나만을 매개 변수로 받으며, 이 배열이 결국 우리가 문제로 받을 배열을 넣어야 한다는 걸 알 수 있겠다.
build_min_heap에게 넘겨주는 매개 변수 n은 최대 인덱스라고 했으니 간단히 매개 변수로 받은 배열의 length-1 값을 넘겨주면 된다.
i <- n downto 2
// 이번엔 최대 인덱스인 n부터 2까지 범위를 설정했다??
이유는 for문 내부의 구현 내용을 보면 알 수 있다. 문제에서의 추가 조건은 최소 힙이 완성됐을 시에 트리에서 가장 꼭대기 노드(첫 번째 인덱스)와 가장 아래 노드(마지막 인덱스)의 위치를 바꾸고, 마지막 인덱스가 된 꼭대기 노드는 고정 시킨 후 남은 노드들로 다시 최소힙을 구성하는 것인데, A[1] <-> A[i] 가 위치를 바꾼 내용이고, 다시 한번 heapify를 수행하는 것은 노드의 위치를 바꾼 후 조건이 망가진 트리를 다시 재조립하는 과정의 이유에 있다.
최소 노드가 배열의 마지막으로 가서 고정됐기 때문에 배열의 마지막 위치를 건들면 안되므로 heapify에는 n 대신 n-1 (i-1)을 건내주어 i가 2가 될 때까지 수행한다. i가 1이라면 노드가 한 개 남았단 뜻으로 더이상 비교할 인덱스가 없기 때문에 종료한다.
이제 마지막으로 문제의 조건을 보자. 교환의 횟수가 K 번째일 때 해당 배열을 반환하란다.
해당 코드에서 교환이 일어나는 경우는 언제가 있을까? 바로 A[1] <-> A[n] 에서 배열의 처음과 끝을 바꾸는 경우와
heapify에서 자식 노드가 부모 노드보다 작을 때 재귀적으로 교환하는 A[k] <-> A[smaller] 경우이다.
그럼 둘 다에서 count++를 더해주고, count가 K가 될 때 멈추자!.. 는 너무 일차원적인 생각이고.
두 경우 다 특정 두 인덱스의 배열 값을 바꿔주는 내용이기 때문에
매개변수로 인덱스 두 개를 받고 서로 바꿔준 후 count를 ++해주는 함수를 만들면 가독성 면에서도 좋고 논리의 흐름에서도 좋겠다.
나와라 최종코드!!!!!
 |
 |
(마지막부에 설명한 특정 인덱스 두 위치를 바꿔주는 함수가 switchArr 함수이다.)
시간 초과가 굉장히 많이 나와서 별에별 방법을 다 사용하느라 코드가 지저분..
시간 초과의 이유는 결국 답의 산출 방식에 있었다. 정답 예시의 포맷에 맞추느라 배열의 값들을 하나씩 꺼내서 String answer에 더했는데, 찾아보니 String의 + 연산은 굉장히 시간이 많이 든다고 한다.
이유는 String은 객체의 변경을 허용하지 않으므로 + 연산 후 이전의 문자열은 레퍼런스를 잃고 가비지 컬렉션에 버려지는데
그게 100번 반복되고, 1000번 반복되고, 10000번 반복되면 버려지는 문자열의 양과 개별 + 연산에 필요한 수많은 시간이 합쳐지므로 시간 초과를 내는 것이다..
그래서 문자열 연산의 시간을 대폭 줄이며 메모리 누수를 막는 클래스 StringBuilder와 .append("문자열") 을 썼더니 뭔 짓을 해도 안 되던 시간초과가 간단히 해결됐다!
이것으로 재밌는 자료구조 형태인 Heap도 해결. 문제는 다 푼 것 같은데 시간초과를 해결 못 해서 업로드가 늦어졌다..
전혀 신경도 않던 수많은 데이터의 입력과 출력에 대해서 좀 더 알게 되어 얻은 건 많은 것 같아!
나를 죽이지 못하는 고통은 나를 강하게 만들 뿐이다.. 더 더 성장하자. 그럼 바힙바힙~
'Algorithm > 백준을 자바라' 카테고리의 다른 글
| [Java] 백준 입출력 템플릿 form (0) | 2024.08.22 |
|---|---|
| 1254번 : 팰린드롬 만들기 (0) | 2023.04.03 |
| 1158번 : 요세푸스 문제 (1) | 2023.03.17 |
| 26008번 : 해시 해킹 (0) | 2023.03.16 |
| 10818번 : 최소, 최대 (2) | 2023.03.15 |




